What Is Difficult to Solve? - Searching Through 180,828 Mate in Two Problems - Part III
It is time to continue the search for the hardest mate in two problems. If you just joined or missed the first two parts you can find them here:
In part one, I asked the readers to solve four mate in two problems. The first problem was a really poor composition in the sense that it had four different first moves that gave mate in two. One of the problems I would like not to end up with. The premise for the selection was a problem with few unique moves in the final position that results in mate. In this case, each of the four moves that gave mate had one checkmating move. As the opposite the second problem had several unique moves that gave mate all decided by the Black move. For problems 3 and 4 the readers were presented with a low and high node-scoring problem.
The plot shows that out of the 44 participants, almost all got problem 1 correct, while the added complexity of more unique checkmating moves gave a small drop in solve rate. Finally, the low node-scoring problem almost all got correct, while the real difficulty was caused by the high node-scoring problem. Only 5 out of 44 got the solution correct! The average time spent by those who got it correct was also around 7 minutes. If you want to give it a try:
Four problems are of course a small sample size, but it goes in hand with the cluster plot I did in part II and my own experience looking at the problems.
The data also suggest that there is no correlation between the other variables (legal moves before mate, legal moves after first move, unique final moves leading to mate, complexity, diversity, open squares around king) that I picked out in regards to a high average node and time score.
Average nodes vs. average time
I have used these two variables to measure the difficulty, and they seem to be the best way to slim down the 178,887 mate in two problems I have after I removed all the not mates in two problems that were present in the collection. But what is the difference? And could we also measure the depth of the engine solution?
Nodes
Definition: Nodes represent the number of unique positions that the engine evaluates. One node equates to one position.
Relation to problem difficulty: The number of nodes searched can indicate the complexity of a problem. More nodes mean the engine had to evaluate more positions before finding the solution. A high number of nodes in finding a mate-in-two could suggest a complex problem with many possible variations to consider.
Nodes and efficiency: High node counts can also reflect on the efficiency of the engine's search algorithm. Some positions might cause the engine to evaluate many unnecessary positions, while others are solved more directly.
Time used in the search
Definition: This is the actual time the engine spends analyzing a position to reach the mate in two solutions.
Time and problem difficulty: Longer analysis times can imply a more complex problem, especially if the engine is set to reach a fixed depth. If it takes longer to find a mate-in-two, the solution might not be obvious, requiring more computational effort.
Time, depth, and nodes: The relationship between time, depth, and nodes isn't linear. An engine might reach a high depth quickly in a simple position but might take longer in a complex position due to the increased number of nodes and the intricacies of the position.
Depth
Definition: In chess engine analysis, depth refers to the number of half-moves (plies) ahead that the engine calculates. For instance, a depth of 10 means the engine looks 10 half-moves (5 moves for each player) into the future.
Relevance to difficulty: A higher depth indicates that the engine needs to look further ahead to find the best moves or solve a problem. In the context of "mate in two" puzzles, if an engine requires a higher depth to find the mating sequence, it implies the solution is less straightforward and potentially more complex since the mate in two is just two moves out in the future.
Depth and Complexity: Depth is a direct measure of the tactical and computational complexity of a position. Positions that require deeper analysis to yield a mate-in-two generally should be more challenging.
Therefore I have decided to run an evaluation on the depth it takes to solve each mate in two problem to add a layer to help with deciding the hardest problems. However, I don’t think it makes sense to use the full dataset anymore, so I have made a normalized score of average nodes and average time and taken the highest 10% to continue with. That is 17,888 problems.
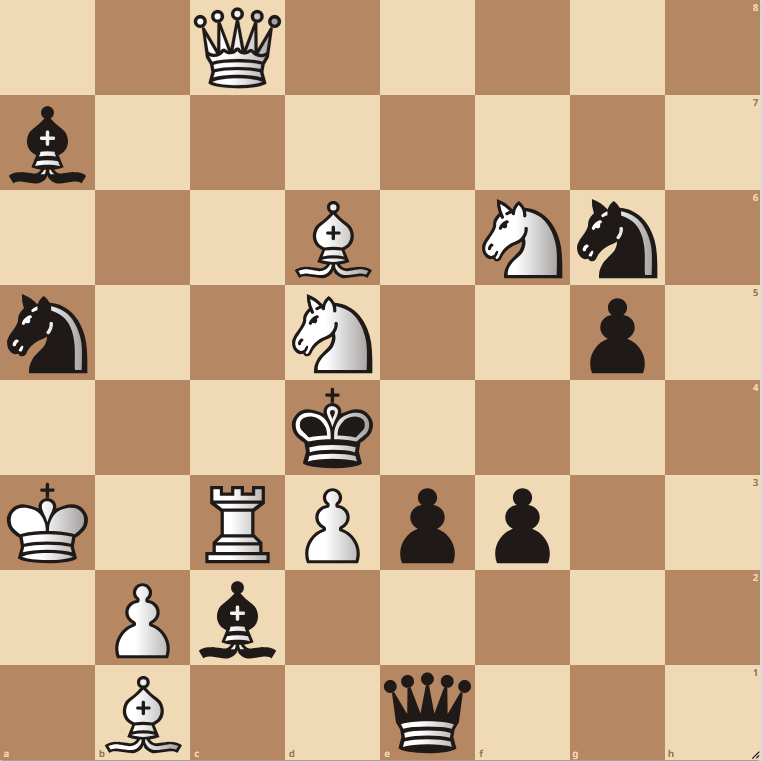
To give a sense of depth. Here is one of the few problems that Stockfish 16 goes to depth 26 before finding the correct move:
It is ranked as number no. 7627 based on the combined nodes and time score. Okay, while writing this the engine just found a problem with depth 31!
I think I will just let you solve this one and then we will continue this series next week!
Have a great weekend!
/Martin








Very interesting research. Maybe I missed something you wrote somewhere or that is somehow implicit or obvious (in the case, I am sorry for the dumb question), but I can not figure out which side is to move in the proposed problems. Always White to move? It depends on the chessboard orientation? TIA.
So I'm one of the only people who got the first problem wrong?
Cool. Cool.