Mate in Two Clustering!? - Searching Through 180,828 Mate in Two Problems - Part II

Learning about t-SNE

I have decided to learn something new in the hunt for the hardest mate in two problems. I asked my brother, who does ai-research if he had any ideas of how to determine the hardest problems based on the variables laid out in the last newsletter. He suggested I try to use t-SNE or t-distributed stochastic neighbor embedding. I had to Google it to find out what it was, but it sounded promising so I decided it was worth learning.

Searching Through 180,828 Mate in Two Problems - Part I

t-SNE is a way of creating a map where similar items cluster together. I’m learning as we go, so the following is as I understand how it works:

1. Gathering the Clues (Loading the Data):

   First, we bring in our data. For this, I used 5,000 mate in two problems I had analyzed. I still need to analyze around 30,000 problems out of the 180,828.

2. Selecting the Important Clues (Preprocessing):

   Out of all the details, I picked the ones I think are most important to understanding the difficulty of the problems. I have selected: average nodes used, legal moves before mate, legal moves after first move', unique final moves leading to mate, average time (s), complexity, diversity, and open squares around king.

3. Putting Clues in Perspective (Scaling):

   To compare the clues fairly, their scale is adjusted. Each detail about the chess problems (like the number of legal moves or the complexity) is like an ingredient with its own scale of measurement. Some details might have small numbers that don't change much, like the number of open squares around the king. Others might have huge numbers that vary widely, like the time taken to solve a problem, which could be anything from a few milliseconds to seconds (for Stockfish).

4. Creating a Map of the Clues (t-SNE):

   With a special technique called t-SNE, we take all our selected details and translate them into a map where similar chess problems are close to each other, and different ones are far apart.

5. Forming Groups (Clustering):

   The problems are then grouped into neighborhoods on the map. Each group, or cluster, has chess problems that are kind of alike. I used a method called KMeans, which finds the center of a group and gathers all the nearby points.

This now creates the following visualization of the chess problem clustering. I have added signs to locate the top 10 and bottom of the variables, so we can get an idea of where they are clustered together.

So how will this help us? The idea should be that we now can use our mate in two map to locate clusters with hard mate in two problems and clusters with problems we dislike or find easy. If you locate cluster 11 you can see that it contains a good share of bottom average nodes used problems, bottom complexity, and bottom diversity. Let’s investigate and have a look at some problems from cluster 11:

3 mate in two problems from cluster 11

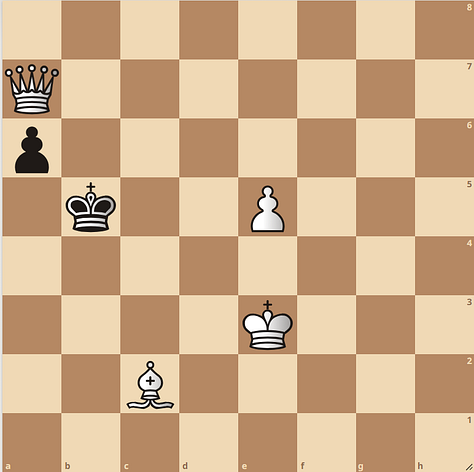
The positions are quite simple with few pieces. If we compare it to some positions from cluster 0, where there are many top average nodes used and top unique moves leading to mate:

3 mate in two problems from cluster 0

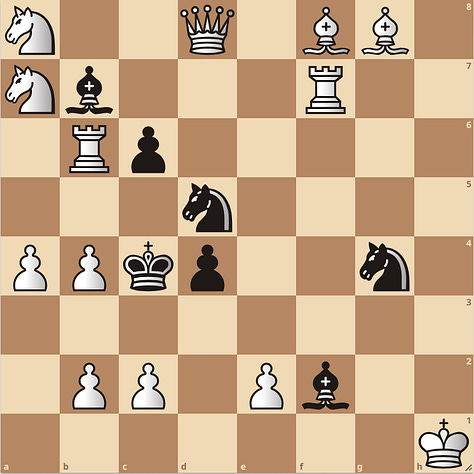
I’m pretty sure that you will find it harder to solve the cluster 0 problems compared to cluster 11. You can give it a try. My current working theory is that the most interesting problems are found in the upper right corner marked with green and the least interesting problems are in the lower left corner marked with red.

I have extracted 5 examples from each cluster so you can have a look. It would be interesting to hear your thoughts about them. Which do you like/dislike, and which cluster do you think has the hardest mate in two problems?

Within the next days, I will have analyzed all 180,828 and I can also share the results of the small survey I did (not too late to try).

Finally, If you want to support my research into the field of mate in two problems I’m offering a 40% discount for a yearly subscription.

/Martin